洛谷9_2选择、冒泡、插入排序及其优化

【模板】排序

题目描述

将读入的 $N$ 个数从小到大排序后输出。

输入格式

第一行为一个正整数 $N$。

第二行包含 $N$ 个空格隔开的正整数 $a_i$，为你需要进行排序的数。

输出格式

将给定的 $N$ 个数从小到大输出，数之间空格隔开，行末换行且无空格。

样例 #1

样例输入 #1

5
4 2 4 5 1

样例输出 #1

1 2 4 4 5

提示

对于 $20\%$ 的数据，有 $1 \leq N \leq 10^3$；

对于 $100\%$ 的数据，有 $1 \leq N \leq 10^5$，$1 \le a_i \le 10^9$。

题解

思路一：选择排序(Selection Sort)

分析思路：

退一步想，首先我们找到最小的数，然后再找到第二小的数，换而言之也就是找到除了第一个数之外的最小的数，以此类推，我们每次要从剩下的$N-i$个数中找到最小的数。

那么如何隔离出已经找出的前$i$个数呢？当然我们可以使用一个数组来存储这些数，但是这样会占用额外的空间，我们可以使用交换的方式来实现。这样在本数组内部就可以实现排序。又因为本身要从小到大排序，所以我们每次找到第i小的数之后，就可以直接将其放在第i个位置上即可。

代码实现与详细注释

#include <iostream>
using namespace std;

int main() {
    int n;
    cin >> n;
    int a[100000];
    for (int i = 0; i < n; i++)
        cin >> a[i];
    for (int i = 0; i < n; i++)
    {
        int minIndex = i;
        for (int j = i + 1; j < n; j++) 
        {
            if (a[j] < a[minIndex]) 
            {
                minIndex = j;
            }
        }
        if (minIndex != i) 
        {
            swap(a[i], a[minIndex]);
        }
    }

    for (int i = 0; i < n; i++) {
        cout << a[i] << " ";
    }
    return 0;
}

测试点结果：

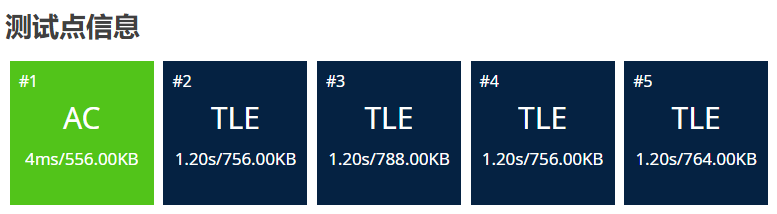
发现测试结果后四题都TLE了，这是为什么呢？

算法分析

每次找到最小值的时间复杂度为$O(n)$，总共要找$n$次，所以总的时间复杂度为$O(n^2)$，这样的时间复杂度对于$10^5$的数据量来说是不可接受的。
虽然比较低效但是我们尽量优化，比如为何一轮不找两个最值呢？

选择排序的双最值优化

优化思路：

我们可以同时找到最大值和最小值，这样可以减少一半的时间，这样的话我们就要将最大值放在最后，最小值放在最前面。但是需要注意的是，如果我们最大值被交换了，那么我们要更新最大值的位置，因为最大值已经被交换到前面了！

代码实现与详细注释

#include <iostream>
using namespace std;
int main() {
    int n;
    cin >> n;
    int a[100000];
    for (int i = 0; i < n; i++)
        cin >> a[i];

    for (int i = 0; i < n / 2; i++) {
        int minIndex = i;
        int maxIndex = i;
        for (int j = i; j < n - i; j++) {
            if (a[j] < a[minIndex]) {
                minIndex = j;
            }
            if (a[j] > a[maxIndex]) {
                maxIndex = j;
            }
        }
        // 交换最小值到前面
        if (minIndex != i) {
            swap(a[i], a[minIndex]);
        }
        // 更新最大值的位置，如果最大值被交换了！！
        if (maxIndex == i) {
            maxIndex = minIndex;
        }
        // 交换最大值到后面
        if (maxIndex != n - i - 1) {
            swap(a[n - i - 1], a[maxIndex]);
        }
    }
    for (int i = 0; i < n; i++) {
        cout << a[i] << " ";
    }
    return 0;
}

测试点结果：

当然，因为渐进时间复杂度还是$O(n^2)$，所以还是TLE了。

思路二：冒泡排序(Bubble Sort)

分析思路：

刚才选择排序是我们人为的遍历找到最小值，那么我们是否可以让最小值自己主动“浮到”最前面呢？显然，要在一个数组中操作又不改变数组的其他值，我们必须要交换来实现，而在选择排序中，我们是每次找到最小值之后就交换，换句话说使我们人为的查了$n-i$次，交换了一次，而为什么不能查一次换一次呢？这就是冒泡排序的思想。
不过，其实从这里我们也可以预料到，查一次换一次坑定比查$n-i$次换一次要慢，所以难怪一般一开始学习排序算法的时候都是冒泡排序，因为虽然甚至比选择排序还要慢，但是它的思想更加直观，更加容易理解。

代码实现与详细注释

#include <iostream>
using namespace std;
int main()
{
    int n;
    cin>>n;
    int a[100000];
    for(int i=0;i<n;i++)
        cin>>a[i];
    for(int i=0;i<n-1;i++)
    {
        for(int j=0;j<n-i-1;j++)//隔离出已经排好序的i个最大数
        {
            if(a[j]>a[j+1])//如果前一个数比后一个数大，就交换，冒上去
            {
                swap(a[j],a[j+1]);
            }
        }
    }
    for(int i=0;i<n;i++)
    {
        cout<<a[i]<<" ";
    }
    return 0;
}

测试点结果：

可以预料的是，冒泡排序的时间复杂度也是$O(n^2)$，在同阶数的情况下，甚至于还比选择排序慢所以这里也是TLE。

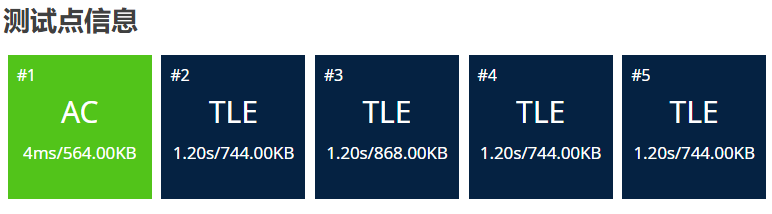
算法分析

基于上面的分析，冒泡排序应该是$O(n^2)$并且比选择排序还要慢，因为每次比较都要交换，而选择排序是遍历比较完了只交换一次。
而有一种冒泡排序的优化方法是如果一轮比较完了没有交换，那么说明已经有序了，就可以直接退出，这样可以减少一些时间，但是最坏情况下还是$O(n^2)$。

冒泡排序的跳过起始有序的优化

#include <iostream>
using namespace std;
int main()
{
    int n;
    cin>>n;
    int a[100000];
    for(int i=0;i<n;i++)
        cin>>a[i];
    for(int i=0;i<n-1;i++)
    {
        bool flag=true;
        //每轮开始前初始化为true默认为有序
        for(int j=0;j<n-i-1;j++)//隔离出已经排好序的i个最大数，以及空出最后一个a[j+1]
        {
            if(a[j]>a[j+1])//如果前一个数比后一个数大，就交换，冒上去
            {
                swap(a[j],a[j+1]);
                flag=false;
                //如果有交换，就将改为false即不完全有序
            }
        }
        if(flag)
            break;
        //如果本轮没有交换，说明已经全部有序，直接退出
    }
    for(int i=0;i<n;i++)
    {
        cout<<a[i]<<" ";
    }
    return 0;
}

明显优化了不少但是还是两个TLE

算法分析

这样的优化方法可以减少一些时间，但是最坏情况下还是$O(n^2)$，因为每次都要遍历一遍，所以最坏情况下还是$O(n^2)$，但是如果数据本身就是有序的，那么时间复杂度就是$O(n)$，所以这样的优化方法还是有一定的效果的。

双向冒泡排序：鸡尾酒排序(Cocktail Sort)

优化思路：

鸡尾酒排序是冒泡排序的一种变种，它是双向的冒泡排序，同时从左到右和从右到左进行冒泡排序，这样可以减少一些时间。

代码实现与详细注释

#include <iostream>
using namespace std;

int main() {
    int n;
    cin >> n; // 读取数组大小
    int a[100000];
    for (int i = 0; i < n; i++)
        cin >> a[i]; // 读取数组元素

    // 双向冒泡排序
    for (int left = 0, right = n - 1; left < right; left++, right--) 
    {
        bool flag = true; // 标记是否有交换
        for (int i = left; i < right; i++) 
        {
            if (a[i] > a[i + 1]) 
            { // 从左到右冒泡
                swap(a[i], a[i + 1]);
                flag = false;
            }
            if (a[n - i - 1] < a[n - i - 2]) 
            { // 从右到左冒泡
                swap(a[n - i - 1], a[n - i - 2]);
            }
        }
        if (flag)
            break; // 如果没有交换，说明已经有序，退出循环
    }
    for (int i = 0; i < n; i++) 
    {
        cout << a[i] << " "; 
    }
    return 0;
}

测试点结果：

算法分析

鸡尾酒排序的时间复杂度也是$O(n^2)$，但是在某些情况下会比冒泡排序快一些，因为它是双向的冒泡排序，所以在某些情况下会比冒泡排序快一些，但是渐进时间复杂度还是$O(n^2)$。

总而言之，我们就是要充分利用已经排好序的的数组能够减少时间复杂度，毕竟现成的有序概率很小，那么我们能不能自己先造一个有序的数组呢？然后充分的利用这个有序的数组呢？这就是下面的插入排序的思想了。从这个角度看，插入排序可以认为是冒泡排序有序跳过优化的再优化，因为是人为制造了有序数组。

思路三：插入排序(Insertion Sort)

分析思路：

那么如果我们不去每轮找到或者冒出最小值或者最大值，还可以咋办呢？我们可以想象一下，我们手里有一副扑克牌，我们要将它们从小到大排序，我们是怎么做的呢？我们从第二张牌开始，如果它比第一张牌小，那么我们就将它插入到第一张牌的前面，如果它比第一张牌大，那么我们就不用动它，然后我们再拿第三张牌，如果它比第二张牌小，那么我们就将它插入到第二张牌的前面，如果它比第二张牌大，再去比较第一张牌，如果它比第一张牌小，那么我们就将它插入到第一张牌的前面，如果它比第一张牌大，那么我们就不用动它，以此类推，我们就可以将这副扑克牌从小到大排序。
转化为抽象语言就是，我们每次拿到一个数，我们将它比较并插入到已经排好序的数组中，这样我们就可以实现排序，这样就充分利用了已经排好序的数组，而不是每次都要遍历找到最小值或者最大值。

动画演示

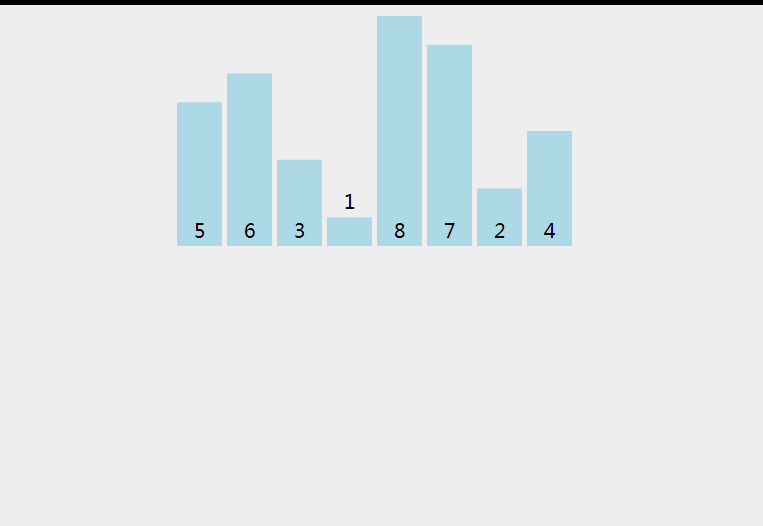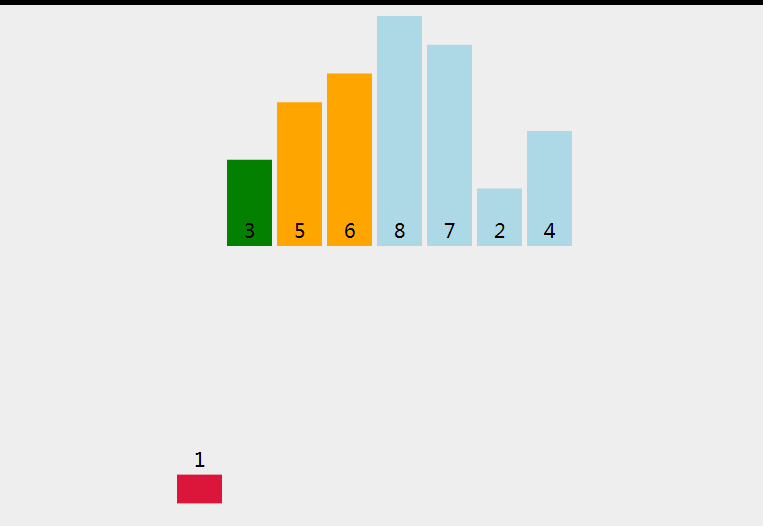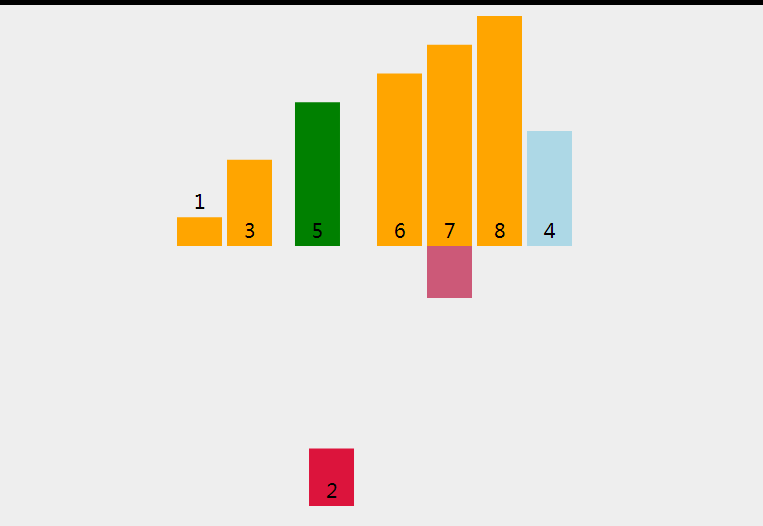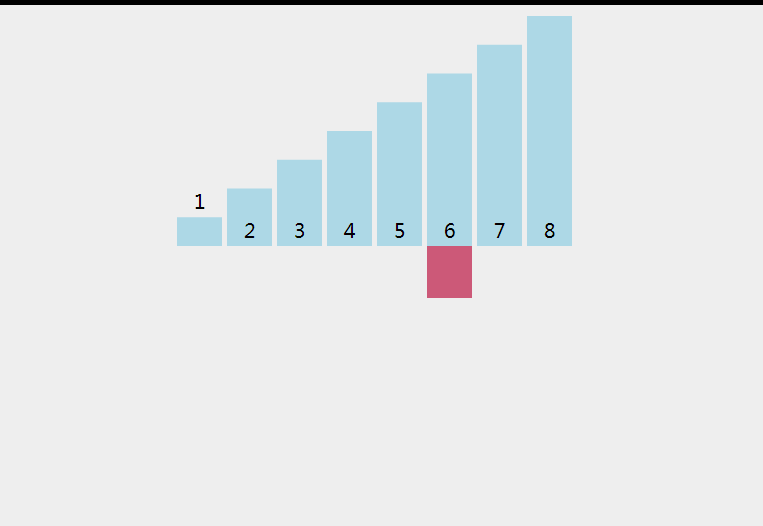
代码实现与详细注释

#include <iostream>
using namespace std;
int main()
{
    int n;
    cin>>n;
    int a[100000];
    for(int i=0;i<n;i++)
        cin>>a[i];
    for(int i=1;i<n;i++)//从第二张牌开始插
    {
        int temp=a[i];
        //因为如果要插入，那么a[i]就要被覆盖，所以要先保存
        int j;
        //而且要知道停止的位置，所以要用一个变量来记录，不妨就用j来记录，因此要在内层for循环外面定义j
        for(j=i-1;j>=0;j--)
        {
            if(a[j]>temp)//从大往小如果该数比a[i]大，就往后挪一个位置
            {
                a[j+1]=a[j];
            }
            else
                break;
        }
        a[j+1]=temp;
        //a[j]比a[i]小自然将a[i]的值插入到内循环后面的数已经空出的废用的a[j+1]的位置
    }
    for(int i=0;i<n;i++)
    {
        cout<<a[i]<<" ";
    }
    return 0;
}

测试点结果：

居然只有一个TLE，这是为什么呢？

算法分析

不难理解由于充分利用了已经排好序的数组，如果数组本身就是有序的，那么时间复杂度就是$O(n)$，但是如果数组是逆序的，那么时间复杂度就是$O(n^2)$，不过如果过程当中有不少顺序的情况那么时间复杂度就会大大短于冒泡排序和选择排序，算是最最基础的排序算法中最快的之一了。

插入排序的二分查找优化(Insertion Sort with Binary Search)

优化思路：

由于每次插入的序列都是有序的，所以我们可以使用二分查找来找到插入的位置，这样可以再次充分利用有序的特性，减少时间复杂度。由于二分查找的时间复杂度是$O(\log n)$，所以这样的优化可以大大减少时间复杂度。所以我们可以将插入排序的时间复杂度降低到最低$O(n\log n)$。预计这样的优化可以通过所有测试点。

代码实现与详细注释

#include <iostream>
using namespace std;
int main()
{
    int n;
    cin>>n;
    int a[100000];
    for(int i=0;i<n;i++)
        cin>>a[i];
    for(int i=1;i<n;i++)//第一个数就一个数默认有序，从第二个数开始插
    {
        int temp=a[i];
        //因为如果要插入，挪动后a[i]就要被覆盖，所以要先保存
        int left=0;
        int right=i-1;
        while(left<=right)
        {
            int mid=(left+right)/2;
            if(a[mid]>temp)//说明插入的位置在左边
                right=mid-1;//更新右边界
            else
                left=mid+1;//反之说明插入得值在右边，更新左边界
        }
        //二分查找a[i]，找到插入的位置
        for(int j=i-1;j>=left;j--)
        {
            a[j+1]=a[j];
        }
        //将插入位置后的每个数往后挪一个位置给temp腾出位置
        a[left]=temp;
        //插入
    }
    for(int i=0;i<n;i++)
    {
        cout<<a[i]<<" ";
    }
    return 0;
}

测试点结果：

和预计的一样，通过了所有测试点。

算法分析

我们成功的利用了二分查找的优化把原来的$O(n^2)$的时间复杂度降低到了接近$O(n\log n)$，这样的时间复杂度对于$10^5$的数据量来说是可以接受的。这便是充分利用有序数组的结果！

总结

• 选择排序、冒泡排序、插入排序都是最最基本排序算法，时间复杂度都是$O(n^2)$，空间复杂度都是$O(n)$，但是插入排序在“基本有序的”情况下会比选择排序和冒泡排序快很多。
• 选择排序是每轮找到最小值之后再交换一次，冒泡排序是每轮比较中每一次都交换，插入排序不是按照原数组比较，而是和已经造好的有序的数组比较，充分利用了中间过程的有序性！
• 9_2算法速度排名：插入排序二分优化>插入排序>选择排序>冒泡排序
• 无一例外这些算法都是基于比较的排序算法，因此时间复杂度的下限最多是$O(n\log n)$，这是由信息论决定的！因此我们要想进一步优化，就要考虑非比较排序算法，比如计数排序（9_1）、桶排序、基数排序等等，不过这些算法都是有一定的局限性的，比如计数排序只能对整数进行排序，桶排序要求数据分布均匀等等。
• 其中最为有效的优化是插入排序的二分查找插入优化！将时间复杂度最多降低到了$O(n\log n)$，那么这样二分的思想我们还可以引出快速排序，归并排序等等，这些都是基于分治思想的排序算法，这些算法的时间复杂度都是最低$O(n\log n)$，是十分高效的排序算法。
• 9_3_1\9_3_2我们将讲述快速排序，归并排序等排序算法，且听下回分解！